Remote state preparation with unit success probability

Quantum information science (QIS) emerged recently as a fascinating engagement between quantum physics and information theory. It is among the top-ten topics over all the branches of science. The revolutionary feature of QIS is that information is stored, transmitted and processed in a quantum way. And, a vital ingredient in a quantum protocol to be superior to a classical one is purely quantum, the so-called quantum entanglement. In other words, by sharing a sufficient amount of quantum entanglement, remote parties are able to execute various interesting tasks only by local operation and classical communication (LOCC). One such task is remote state preparation (RSP) [1–3] in which a party, Alice, needs securely and faithfully to prepare a quantum state , known to her, for a remote party, Bob, who has absolutely no knowledge about . The first original protocol for RSP of a single-qubit state was proposed explicitly in [2]. Since then it has been extended to various more involved scenarios, such as RSP of multiqubit states [4], an ensemble of states [5] and states in higher dimensions [6]. Experiments on RSP have also been reported in [7]. In general, all of the existing RSP protocols succeed only with probabilities of less than 100%, i.e. they are probabilistic.

In this paper, we are concerned with the question 'can one make a general RSP successful with unit probability?' For that purpose, we reconsider the original probabilistic protocol in [2] and try to make it deterministic. To achieve this goal, some additional resource/operation will be needed. However, as we shall show, such additional ingredients are just local ones (e.g. ancillary qubits, local operations) or of a classical nature (e.g., the conventional media), which are commonly regarded as low cost. The greatest cost is due to the shared quantum resource, which in our protocol is the same as in the probabilistic one [2]. Therefore, the net benefit is the possibility of achieving unit success probability at the expense of cheap additional ingredients. In section 2, we represent the original protocol of [2] for RSP of the most general single-qubit state to see that it is just probabilistic. Then, in section 3, we design our deterministic protocol. Finally, we draw our conclusion in section 4.

Let the most general single-qubit state that Alice needs, only by means of LOCC, to prepare for a remote Bob be

with the two orthonormal states of a qubit in the computational basis and satisfying the normalization condition . Since the quantum measurement postulate does not allow for distinguishing quantum states that differ only by a global phase factor, we can, without any loss of generality, set α=a and with a, b, φ∈R and a²+b²=1. Then the state (1) is rewritten as

Suppose that Alice knows all of the parameters a, b and φ precisely, but Bob knows nothing. According to the protocol in [2], Alice and Bob should share a pair of maximally entangled qubits of, say, the form

of which Alice possesses qubit A and Bob qubit B. Since Alice knows a, b and φ, she is fully able to measure her qubit in any basis determined by those parameters. Let such a basis be

with

It is clear that the transformation M is unitary and forms a complete orthonormal set of states of a qubit in Hilbert space of dimension 2. When Alice measures the qubit A in the basis , the outcome or occurs at random, but each of them has a probability of 1/2. If it is Bob's qubit B collapses into

from which Bob cannot reconstruct , equation (2), because of his lack of knowledge of the necessary parameters, implying a failure. However, if Alice obtains , the collapsed state of the qubit B is

from which Bob can reconstruct , by applying on the operator σ_x σ_z (σ_x ={{0,1}, {1,0}} is the Pauli bit-flip operator and σ_z ={{1,0}, {0,−1}} the Pauli phase-flip one). Knowledge of the parameters a, b,φ does not matter at all. For Bob to perform the right action, Alice is required to announce her outcome, say, via a public classical communication channel. Since there are two possible outcomes, or , the classical communication cost (CCC) is just 1 bit. As for the success probability, it is P=50%. That is to say, this protocol is probabilistic.

In this section, we aim to design a deterministic protocol based on the same shared quantum channel as in [2]. For the protocol to always succeed, an additional local quantum resource/operation and CCC must be consumed. Given the same shared quantum channel , equation (3), as a starting point like in [2], our protocol works as follows.

Firstly, Alice takes an ancillary qubit in state .

Secondly, she performs a controlled-NOT gate (CNOT) on the qubits A and , with A the control qubit and the target one (i.e. , with i, j∈0, 1 and ⊕ an additional mod 2). As a result, the channel and the state become an entangled state . It is worth emphasizing that the state need not be shared beforehand at all; it is made locally by Alice from the quantum channel state .

Thirdly, Alice measures the qubits A and in different bases. For the qubit A, the measurement basis is defined as

with

while for the qubit the basis is

with

Note that Alice is in full manipulation of the bases (8) and (10) since she knows their determining parameters (a, b) and φ. A wise strategy Alice adopts is to measure the qubits A and in sequence. In other words, she postpones measuring the qubit until after she obtains the outcome of measuring the qubit A. When measuring the qubit A in the basis , if is found, the unmeasured qubits and B collapse into the (unnormalized) state,

In this case, Alice does not measure the qubit immediately but applies to it a unitary phase-shift operator,

thus transforming to

Only after that operation does Alice measure the qubit in the basis Expressed in terms of , the state (14) reads

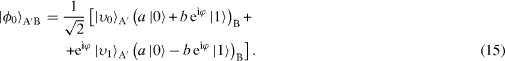
With an equal probability, Alice may find when measuring the qubit A. This event projects the qubits and B onto the (unnormalized) state

In this case, Alice immediately proceeds to measuring the qubit in the basis , in terms of which the state (16) reads

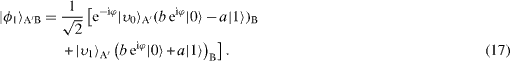
Fourthly, Alice broadcasts 2 bits for identifying her four possible measurement outcomes in the following way: '00', '01', '10' or '11', if she found or respectively. Transparently, if Alice's announcement is '00', Bob's qubit B is left exactly in the desired state, equation (2). If it is '01', Bob's qubit B is, up to a global phase factor, in the state , which he can easily transform to the desired one by applying a phase-flip operator σ_z . If '10' is broadcast, Bob is sure that his qubit is, up to a global phase factor, in the state , which requires application of both phase- and bit-flip operators σ_x σ_z . Finally, the outcome corresponding to '11' projects Bob's qubit onto the state , which is nothing else but the desired one, up to a bit-flip operator σ_x . As seen from equations (15) and (17), each of Alice's outcome happens randomly but with an equal probability of 1/4. Since Bob is always able to recover the desired state (2), the total success probability is P=(1/4)×4=100%, rendering our protocol a deterministic one.

In other words, here the strategy of adaptive or feedforward measurements applies. 'Adaptive' or 'feedforward' means sequential measurements that should be performed one by one in such a way that the outcome of a given measurement decides the basis of the next measurement. If measurements of the qubit A in the basis (see equation (8)) and of the qubit in the basis (see equation (10)) are carried out independently, then we can write

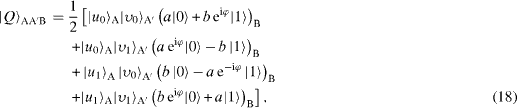
which implies success with a probability P=50% when Alice's measurement yields . However, with the strategy of adaptive measurements, the first measurement is to be done on the qubit A in the basis , whose outcome is specified by m=0 (1) if is found. Then, the basis for the second measurement to be done on the qubit ^A' depends on the outcome m in the following manner:

where , with V and Π given by equations (11) and (13). If the outcome of the first measurement is , with m=0 or 1, and that of the second corresponding measurement is , with n=0 or 1, then the eventually collapsed state of the three qubits A, and B is , from which it follows that the outcome-dependent recovery operator is , for any , implying P=100%.

We have designed a protocol for RSP of the most general single-qubit state employing the same shared quantum channel, i.e. one maximally entangled state of two qubits, as in [2]. However, we let the preparer use one ancillary qubit and be capable of locally performing a CNOT on that qubit and the qubit belonging to the shared entangled state as well as measuring the ancillary qubit. These boost the success probability of our protocol to P=100%, as compared with P=50% of that proposed in [2]. Our CCC is, however, 2 bits. The salient merit of our protocol is the achievement of unit success probability via the same nonlocal quantum resource previously shared between the preparer and the receiver. This matters significantly because the added ingredients are all local or of classical nature whose cost is much cheaper than the cost of the shared nonlocal entanglement and the value of success probability is of paramount importance to assess a quantum protocol. We conjecture that success probabilities of RSP in other more complicated situations could also be boosted considerably provided that additional local resources/operations are employed judiciously.

Before ending, a remark is in order. Of course, state (2) can be transmitted by means of teleportation [8] via the same previously shared quantum channel (3), with P=100% and CCC=2 bits, too. In other words, Alice first applies the operator M defined in equation (5) on the state to have . Then, she executes the standard teleportation protocol proposed for the first time in [8], which requires one CNOT AA', one Hadamard gate H A' and two single-qubit measurements, and , on the qubits A and A' in their computational bases. In total, the operations needed for teleportation are one CNOT AA', two unitary transformations (M A' and H A') plus two measurements and . As measuring an arbitrary single-qubit state in a basis with X any 2×2 unitary operator is tantamount to measuring the state in the computational basis , the operations required for our deterministic RSP protocol, in comparison with those in teleportation, are one CNOT AA', two unitary transformations ( defined in equation (9) and defined in equation (19)), and also plus two measurements in the computational bases ( and ). Therefore, our protocol is at least an alternative to teleportation from the operational point of view, but it proves to be interesting from the RSP conceptual point of view when the complete data set (a, b, φ) of the state to be transmitted is known.