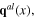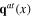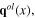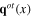Abstract
This work is devoted to the construction of the quantum field theory of the interacting system of plasmons, photons and phonons on the basis of general fundamental principles of electrodynamics and quantum field theory of many-body systems. Since a plasmon is a quasiparticle appearing as a resonance in the collective oscillation of the interacting electron gas in solids, the starting point is the total action functional of the interacting system comprising electron gas, electromagnetic field and phonon fields. By means of the powerful functional integral technique, this original total action is transformed into that of the system of the quantum fields describing plasmons, transverse photons, acoustic as well as optic longitudinal and transverse phonons. The collective oscillations of the electron gas is characterized by a real scalar field φ(x) called the collective oscillation field. This field is split into the static background field φ0(x) and the fluctuation field ζ(x). The longitudinal phonon fields 
 are also split into the background fields
are also split into the background fields 
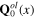 and dynamical fields
and dynamical fields 
 while the transverse phonon fields
while the transverse phonon fields 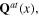
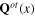 themselves are dynamical fields
themselves are dynamical fields 
 without background fields. After the canonical quantization procedure, the background fields φ0(x),
without background fields. After the canonical quantization procedure, the background fields φ0(x), 
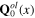 remain the classical fields, while the fluctuation fields ζ(x) and dynamical phonon fields
remain the classical fields, while the fluctuation fields ζ(x) and dynamical phonon fields 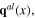
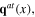
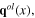
 become quantum fields. In quantum theory, a plasmon is the quantum of Hermitian scalar field σ(x) called the plasmon field, longitudinal phonons as complex spinless quasiparticles are the quanta of the effective longitudinal phonon Hermitian scalar fields
become quantum fields. In quantum theory, a plasmon is the quantum of Hermitian scalar field σ(x) called the plasmon field, longitudinal phonons as complex spinless quasiparticles are the quanta of the effective longitudinal phonon Hermitian scalar fields 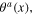
 while transverse phonons are the quanta of the original Hermitian transverse phonon vector fields
while transverse phonons are the quanta of the original Hermitian transverse phonon vector fields 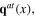
 By means of the functional integral technique the original action functional of the interacting system comprising electron gas, electromagnetic field and phonon fields is transformed into the total action functional of the resultant system comprising plasmon scalar quantum field σ(x), longitudinal phonon effective scalar quantum fields
By means of the functional integral technique the original action functional of the interacting system comprising electron gas, electromagnetic field and phonon fields is transformed into the total action functional of the resultant system comprising plasmon scalar quantum field σ(x), longitudinal phonon effective scalar quantum fields 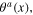
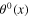 and transverse phonon vector quantum fields
and transverse phonon vector quantum fields 
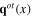 .
.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Since the early works on the collective motion of charged particles in plasma, including the interacting electron gas in solids, it was shown that there exists a resonance of the collective oscillations at some frequency called the plasma frequency. This resonance phenomenon was interpreted as the appearance of an elementary excitation—a complex quasiparticle called a plasmon—and the plasma frequency was also called plasmon frequency (the references on early works on plasmons can be found in the literature [1–3]). In the physical processes with the presence of plasmon the plasmon–photon interaction plays the main role. Moreover, in the electron gas of solids there always exists the electron–phonon interaction leading to the effective plasmon–phonon interaction. Therefore the knowledge on the mutual interaction of plasmon, photon and phonons is necessary for both theoretical and experimental studies on the physical processes and phenomena involving plasmon. The present work is devoted to the elaboration of the quantum field theory of the plasmon–photon–phonon interacting system by applying the functional integral technique [4–7]. The assumptions comprise only the fundamental principles of electrodynamics and quantum theory of many-body system.
For the application of mathematical tools of functional integral technique, the physical content of the theory of phonons in solids must be presented in the languages of the quantum field theory. This will be done in section 2. Here there is a distinction between longitudinal and transverse phonons. While the transverse phonons are described by the transverse phonon vector fields as other transverse vector fields in the theory of the elementary particles, for simplifying the presentation of the formulae related to longitudinal phonons we propose to describe them by some effective scalar fields similar to the quantum fields of spinless particles. Moreover, because the interaction of longitudinal phonons with electron is much stronger than that of transverse ones, in the study of physical phenomena and processes with the dominant competition of longitudinal phonons we can neglect the contribution of transverse phonons. Thus the transverse phonon fields will be retained only in the particular cases when they play the essential role.
Section 3 is devoted to the establishment of the expression of total action functional of the interacting plasmon–photon–phonons system. It contains all three types of fields: (i) collective oscillation field φ(x); (ii) transverse electromagnetic vector field A(x) and (iii) all phonon fields, both acoustic and optic phonon fields 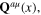
 index μ labeling the phonon branches. By grouping suitable terms from the formula of total action functional of the whole system it is possible to derive expressions of action functional of different subsystems of related fields. The fundamental subsystem is the collective oscillation field φ(x). A short review of the results of previous works related to this field in the harmonic approximation is presented.
index μ labeling the phonon branches. By grouping suitable terms from the formula of total action functional of the whole system it is possible to derive expressions of action functional of different subsystems of related fields. The fundamental subsystem is the collective oscillation field φ(x). A short review of the results of previous works related to this field in the harmonic approximation is presented.
The construction of quantum fields of interacting plasmon–phonon system is the content of section 4. In the harmonic approximation with respect to the collective oscillation field as well as to the fields of both acoustic and optic phonons, the action functional of the subsystem comprising interacting collective oscillation field φ(x) as well as both acoustic and optic phonon fields 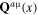 and
and  is derived. Each of longitudinal phonon fields
is derived. Each of longitudinal phonon fields 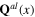 and
and 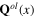 is split into two parts, background field
is split into two parts, background field  or
or 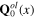 and dynamical field
and dynamical field  or
or 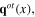 while transverse phonon fields
while transverse phonon fields 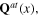
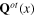 themselves are dynamical ones
themselves are dynamical ones 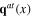 and
and  The dynamical phonon fields generate the physical phonons playing the role of dynamical quasiparticles in physical phenomena and processes.
The dynamical phonon fields generate the physical phonons playing the role of dynamical quasiparticles in physical phenomena and processes.
The construction of the quantum fields of the whole interacting plasmon–photon–phonon system is the content of the section 5. The expression of total action functional of this whole system, described by background fields φ0(x), 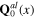 and
and 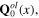 fluctuation field ζ(x), electromagnetic field A(x) and dynamical phonon fields
fluctuation field ζ(x), electromagnetic field A(x) and dynamical phonon fields 
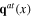 and
and 
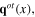 is derived in the harmonic approximation with respect to each of three types of fields: (i) fluctuation field, (ii) electromagnetic field and (iii) all dynamical phonon fields. The characterizing features of different subsystems of the whole system are briefly investigated. From the obtained expression of total action functional of the whole system it is possible to derive the expressions of the action functional of different interaction vertices. The conclusion and discussions are presented in section 6.
is derived in the harmonic approximation with respect to each of three types of fields: (i) fluctuation field, (ii) electromagnetic field and (iii) all dynamical phonon fields. The characterizing features of different subsystems of the whole system are briefly investigated. From the obtained expression of total action functional of the whole system it is possible to derive the expressions of the action functional of different interaction vertices. The conclusion and discussions are presented in section 6.
2. Phonon quantum fields
For using in the study of the interaction of phonons with other quasiparticles in solids by means of the functional integral technique let us construct the quantum fields of phonons. There exist many types of phonons with various characteristics in different materials [8]. In the present work we limit to the frequently investigated solids: elastic media [3] and crystalline lattices [3, 9]. The quantum fields of acoustic and optic phonons will be constructed separately. For simplifying formulae we use the notations proposed in our previous works [4–6] and the unit system with 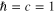 .
.
Consider first the acoustic phonons. In both above-mentioned types of solids there exist one longitudinal and two transverse acoustic phonon branches. Denote  their quantum fields, where μ = 1, 2 for transverse phonons and μ = 3 for longitudinal one. For a definite μth branch between angular frequency ω and wave vector k at small values of
their quantum fields, where μ = 1, 2 for transverse phonons and μ = 3 for longitudinal one. For a definite μth branch between angular frequency ω and wave vector k at small values of 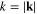 there exists a linear relation
there exists a linear relation
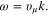
We assume that this formula is the dispersion law of the acoustic phonon in general. It looks like that of a massless relativistic particle, except for the scaling of spatial coordinates
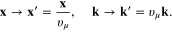
On the basis of the analogy with the free field of relativistic massless particles we have following Lagrange function and action functional of the acoustic phonon in μth branch

and
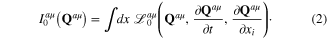
Now we consider the optic phonons. In a crystalline lattice with s non-equivalent ions per a primitive cell, 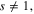 beside three acoustic phonon branches there exist 3(s-1) branches of optic phonons with non-vanishing limiting angular frequency Ωμ at k = 0. Denote
beside three acoustic phonon branches there exist 3(s-1) branches of optic phonons with non-vanishing limiting angular frequency Ωμ at k = 0. Denote  the optic phonon field in the μth branch. Since k-dependent terms in the dispersion law of optic phonon are very small in comparison with the constant terms Ωμ, let us neglect them. Then the optic phonon field
the optic phonon field in the μth branch. Since k-dependent terms in the dispersion law of optic phonon are very small in comparison with the constant terms Ωμ, let us neglect them. Then the optic phonon field  has following Lagrange function and action functional
has following Lagrange function and action functional
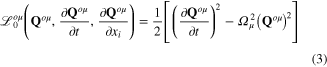
and
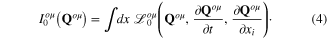
In the special case of isotropic crystals with s = 2 non-equivalent ions per a primitive cell, there exist one longitudinal and two degenerate transverse optic phonon branches with limiting angular frequencies Ωl and Ωt at k → 0. Between Ωl and Ωt there exists following relation
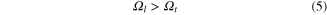
and
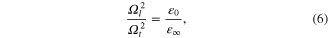
where  0 is the static dielectric constant of the medium and
0 is the static dielectric constant of the medium and 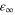 is the square of the refractive index of the medium at optical frequencies.
is the square of the refractive index of the medium at optical frequencies.
In solids there always exists the electron-phonon interaction. In most cases the interaction of longitudinal acoustic or optic phonons with electron is much stronger than that of transverse acoustic or optic phonon, respectively. In these cases the longitudinal phonons play a much more important role than the corresponding transverse phonons do, so that the interaction between longitudinal phonons and electron has been intensively studied during a long time. It was shown that for various solids the Hamiltonians of the interaction between electron and longitudinal acoustic and optic phonons have following expression [3, 9]
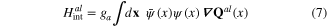
and
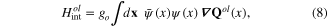
where  is the electron field operator,
is the electron field operator, 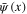 is its Hermitian conjugate. The coupling constants ga and go depend on the crystalline and electronic structures of solids.
is its Hermitian conjugate. The coupling constants ga and go depend on the crystalline and electronic structures of solids.
Meanwhile, the interaction between electron and transverse phonons was much less known. Let us consider the simple case of the lattice with 2 non-equivalent ions per a primitive cell, s = 2. Then beside the two degenerate acoustic transverse phonon branches with wave function  there exist also only two degenerate optic phonon branches with wave function
there exist also only two degenerate optic phonon branches with wave function 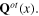 Since the physical origin of the appearance of phonons is the oscillation of ions in solids and the coupling of phonons with electron is caused by the photon exchange between ion and electron, it is natural to believe that the Hamiltonian of the interaction between transverse phonons with electron have the expressions similar to the electron-photon interaction Hamiltonian in the transverse gauge. Therefore we assume following expressions of the transverse phonon–electron interaction Hamiltonians:
Since the physical origin of the appearance of phonons is the oscillation of ions in solids and the coupling of phonons with electron is caused by the photon exchange between ion and electron, it is natural to believe that the Hamiltonian of the interaction between transverse phonons with electron have the expressions similar to the electron-photon interaction Hamiltonian in the transverse gauge. Therefore we assume following expressions of the transverse phonon–electron interaction Hamiltonians:
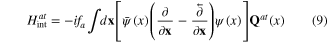
for acoustic transverse phonon and
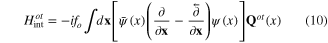
for optic transverse phonon.
The interaction of ions in the lattice with the electromagnetic wave, in principle, can also generate the direct coupling of electron with transverse acoustic and optic phonons. In the transverse gauge the effective interaction Hamiltonians have the expressions
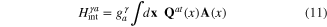
for acoustic phonon and
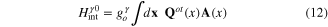
for optic phonon.
3. Total functional integral
As the extension of total functional integral of the interacting plasmon–photon system studied in the previous work [14] we have following total functional integral of the plasmon–photon–phonon system
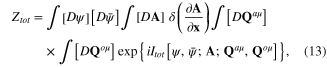
where ![${{I}_{tot}}\left[ \psi ,\bar{\psi };{\bf A};{{{\bf Q}}^{a\mu }},{{{\bf Q}}^{o\mu }} \right]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn56.gif) is the total action functional of this system:
is the total action functional of this system:
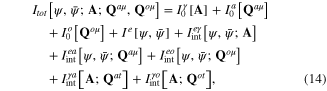
![$I_{0}^{\gamma }\left[ {\bf A} \right]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn57.gif) is the action functional of the transverse free electromagnetic field in the transverse gauge
is the action functional of the transverse free electromagnetic field in the transverse gauge
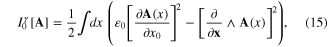
 0 being the static dielectric constant of the medium,
0 being the static dielectric constant of the medium, ![$I_{0}^{a}\left[ {{{\bf Q}}^{a\mu }} \right]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn58.gif) and
and ![$I_{0}^{o}\left[ {{{\bf Q}}^{o\mu }} \right]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn59.gif) are the action functional of two systems of all acoustic phonon fields and all optic phonon fields, respectively
are the action functional of two systems of all acoustic phonon fields and all optic phonon fields, respectively

![$I_{0}^{a\mu }\left[ {{{\bf Q}}^{a\mu }} \right]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn60.gif) and
and ![$I_{0}^{o\mu }\left[ {{{\bf Q}}^{o\mu }} \right]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn61.gif) being determined by formulae (1)–(4),
being determined by formulae (1)–(4), ![${{I}^{e}}\left[ \psi ,\bar{\psi } \right]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn62.gif) is the action functional of the system of electrons mutually interacting through the Coulomb repulsion.
is the action functional of the system of electrons mutually interacting through the Coulomb repulsion. ![${{I}^{e}}\left[ \psi ,\bar{\psi } \right]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn63.gif) consists of two parts
consists of two parts
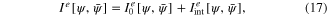
where ![$I_{0}^{e}\left[ \psi ,\bar{\psi } \right]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn64.gif) is the action functional of free electron moving in the electrostatic field of ions in the crystalline lattice
is the action functional of free electron moving in the electrostatic field of ions in the crystalline lattice

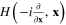 is the quantum mechanical Hamiltonian of single electron
is the quantum mechanical Hamiltonian of single electron
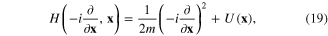
m is the effective mass of electron, ![$I_{\operatorname{int}}^{e}\left[ \psi ,\bar{\psi } \right]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn66.gif) is the action functional of electron-electron Coulomb interaction
is the action functional of electron-electron Coulomb interaction
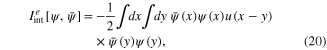
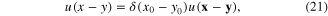
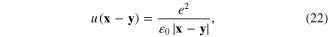
−e is the electron charge. It is straightforward to show that
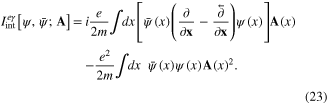
According to formulae (7)–(10) for the electron–phonon interaction Hamiltonians we have
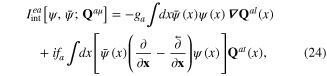
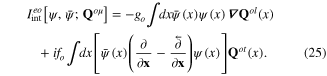
From expression (11) and (12) of the Hamiltonians describing the coupling of transverse phonons with photon it follows that
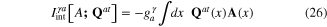
and
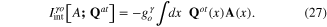
The Coulomb interaction functional (20) is bilinear with respect to the electron density 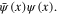 This expression can be linearized by means of the Hubbard-Stratonovich transformation
This expression can be linearized by means of the Hubbard-Stratonovich transformation
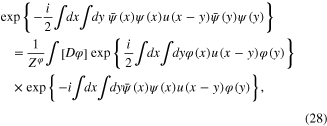
where
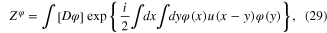
as this was proposed in references [4, 5]. The bosonic real integration variable φ(x) describing collective oscillations of electron gas was called the collective oscillation field. Using formulae (14), (17) and (28), we rewrite the total functional integral (13) in the new form
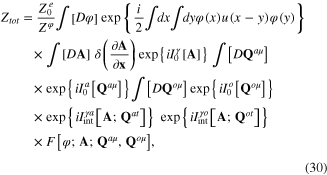
where

and
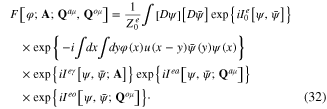
Expanding four last exponential functions in rhs of relation (32) into power series, neglecting the very small terms proportional to 1 m−2 and performing the functional integration over the Grassmann variables, after lengthy but standard calculations we obtain following expression of the functional (32)
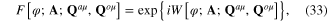
where ![$W[\varphi ;{\bf A};{{{\bf Q}}^{a\mu }},{{{\bf Q}}^{o\mu }}]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn68.gif) is a functional power series of φ(x), Aμ(x), Qaμ(x), Qoμ(x) as the functional variables:
is a functional power series of φ(x), Aμ(x), Qaμ(x), Qoμ(x) as the functional variables:
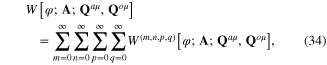
the term ![${{W}^{(m,n,p,q)}}[\varphi ;{\bf A};{{{\bf Q}}^{a\mu }},{{{\bf Q}}^{o\mu }}]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn69.gif) being a homogeneous functional polynome of mth, nth, pth, qth orders with respect to the functions φ(x), A(x), Qaμ(x), Qoμ(x), respectively. Substituting expression (33) of functional
being a homogeneous functional polynome of mth, nth, pth, qth orders with respect to the functions φ(x), A(x), Qaμ(x), Qoμ(x), respectively. Substituting expression (33) of functional ![$F[\varphi ;{\bf A};{{{\bf Q}}^{a\mu }},{{{\bf Q}}^{o\mu }}]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn70.gif) into rhs of formula (30), we transform the total functional integral Ztot of the system of four interacting fields φ(x), Aμ(x), Qaμ(x), Qoμ(x) into the form
into rhs of formula (30), we transform the total functional integral Ztot of the system of four interacting fields φ(x), Aμ(x), Qaμ(x), Qoμ(x) into the form
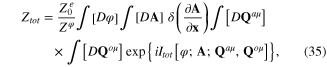
where the total action functional ![${{I}_{tot}}[\varphi ;{\bf A};{{{\bf Q}}^{a\mu }},{{{\bf Q}}^{o\mu }}]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn71.gif) of this system has following expression
of this system has following expression
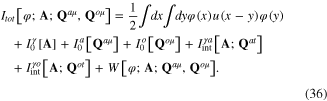
Since the functional ![$W[\varphi ;{\bf A};{{{\bf Q}}^{a\mu }},{{{\bf Q}}^{o\mu }}]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn72.gif) is a series of the form (34), the total action functional of the interacting system of four fields φ(x), Aμ(x), Qaμ(x) and Qoμ(x) has following expression
is a series of the form (34), the total action functional of the interacting system of four fields φ(x), Aμ(x), Qaμ(x) and Qoμ(x) has following expression
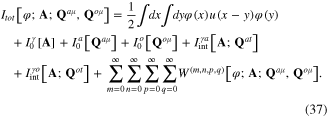
By grouping suitable terms from the expression in rhs of formula (37), we can derive the expression of total action functional of any subsystem of above-mentioned interacting system of four fields φ(x), Aμ(x), Qaμ(x) and Qoμ(x).
The first subsystem is the collective oscillation field φ(x). In references [4, 5] it was shown that this field is split into two parts

where φ0(x) is the static background field, φ0(x) = φ0(x,t) = φ0(x) corresponding to the extreme value of the action functional I0[φ] of this field in the harmonic approximation
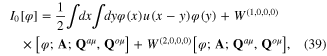
and ζ(x) is the field of small fluctuations around background field φ0(x). We call ζ(x) the fluctuation field. In terms of φ0(x) and ζ(x) the action functional I0[φ] has the expression

where
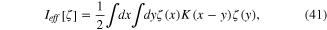

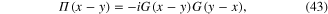
G(x − y) is the two-point Green function of free electron. Denote ![$\tilde{\zeta }[{\bf k},\omega ]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn73.gif) and
and ![$\tilde{K}[{\bf k},\omega ]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn74.gif) the Fourier transforms of the field ζ(x) and the kernel K(x − y). It was known that in the case of a homogeneous electron gas
the Fourier transforms of the field ζ(x) and the kernel K(x − y). It was known that in the case of a homogeneous electron gas
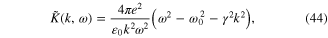
where ω0 is the plasma frequency of the electron gas
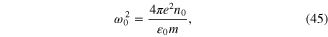
n0 is the electron density and
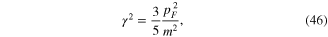
pF is the electron momentum at the Fermi surface. In terms of the Fourier transforms ![$\tilde{\zeta }[{\bf k},\omega ]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn75.gif) and
and ![$\tilde{K}[{\bf k},\omega ]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn76.gif) formula (73) becomes
formula (73) becomes

Setting
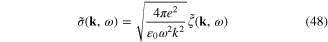
and introducing the scalar field 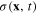 with the Fourier transforms
with the Fourier transforms 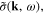 we rewrite
we rewrite ![${{I}_{eff}}[\zeta ]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn79.gif) in the new form
in the new form
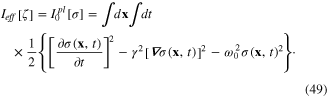
Functional (49) is the action functional of free plasmon field. It has the form similar to the action functional of the Klein–Gordon real scalar field in relativistic quantum field theory [10–13], except for a scaling factor γ at the spatial coordinates. After the canonical quantization procedure, real scalar field 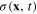 becomes a Hermitian quantum field, whose quantum is plasmon: the quantum plasmon field. The expression of
becomes a Hermitian quantum field, whose quantum is plasmon: the quantum plasmon field. The expression of  in terms of the destruction and creation operators of plasmon was known.
in terms of the destruction and creation operators of plasmon was known.
Thus the quantum plasmon field based on the study of collective oscillation field φ(x) as the fundamental subsystem has been constructed. Another important subsystem is that of phonon fields developed in the preceding section 2. The quantum fields of interacting plasmon–photon subsystem were also constructed in reference [14]. The quantum field theory of plasmon–phonon subsystem is the subject of the next section.
4. Quantum fields of interacting plasmon–phonon system
Now we study in detail the interacting plasmon–phonon system. In order to avoid lengthy expression we limit to the harmonic approximation with respect to two types of fields: (i) the collective oscillation field and (ii) both acoustic and optic phonon fields. Moreover, since the interaction of longitudinal phonons with electron is much stronger than that of transverse phonons, we can neglect the contribution of transverse phonons in the phenomena and processes in which there exists the competition of longitudinal phonons, and retain the electron–transverse phonon interaction only when the transverse phonons play the essential role. In particular, the contribution of transverse phonons must be taken into account when we consider the phenomena and processes with the participation of the transverse electromagnetic field, as this will be performed in the next section.
First we note that the electron–phonon interaction leads to the interaction of phonons with the collective oscillation field. The action functional of the interaction between the fields φ(x), Qaμ(x), Qoμ(x) has the expression of the form
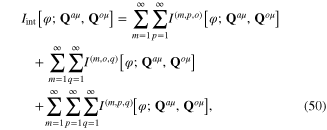
where
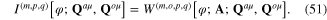
Because the plasmon is the quasiparticle generated by the fluctuation ζ(x) around the background field φ0(x), the state φ0(x) must be considered as the physical vacuum of the plasmon field. Therefore the term ![${{I}_{\operatorname{int}}}[{{\varphi }_{0}};{{{\bf Q}}^{a\mu }},{{{\bf Q}}^{o\mu }}]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn82.gif) must be included into the total action functional of the subsystem comprising only phonon fields
must be included into the total action functional of the subsystem comprising only phonon fields 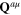 and
and 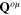 :
:

In order to avoid the lengthy and complicated formulae and as the simple example, let us limit to the first order approximation (m = 1) with respect to the field φ0(x) in the expression (50) of ![${{I}_{\operatorname{int}}}[{{\varphi }_{0}};{{{\bf Q}}^{a\mu }},{{{\bf Q}}^{o\mu }}].$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn85.gif) Then in the harmonic approximation with respect to the phonon fields (p + q ≤ 2) we have following action functional of the subsystem of phonon fields
Then in the harmonic approximation with respect to the phonon fields (p + q ≤ 2) we have following action functional of the subsystem of phonon fields 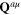 and
and  interacting with the background field φ0(x) of the collective oscillations of the interacting electron gas
interacting with the background field φ0(x) of the collective oscillations of the interacting electron gas
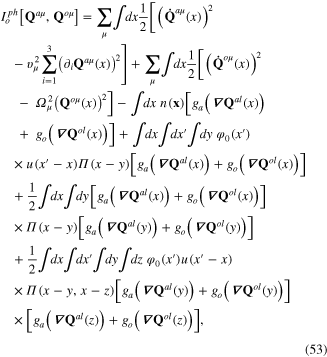
where

It consists of two parts

where the first part
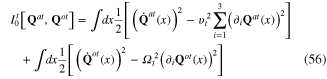
is the action functional of the free transverse phonons, and
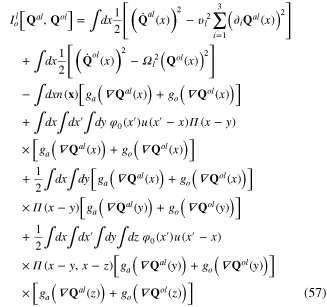
is the total action functional of the acoustic as well as optic longitudinal phonons interacting with the background field φ0(x) of collective oscillation field φ(x). The interaction action functional in this expression leads to the mixing between acoustic and optic phonons.
From the extreme action principle
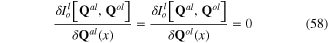
it follows the system of differential-integral equations for the background phonon fields 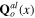 and
and  corresponding to the extreme value of the action functional (57):
corresponding to the extreme value of the action functional (57):
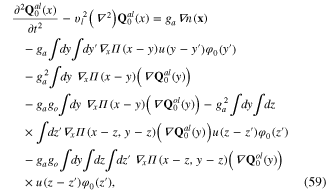
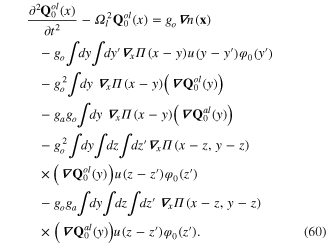
Denote 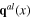 and
and 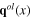 the small fluctuations of the longitudinal phonon fields
the small fluctuations of the longitudinal phonon fields  and
and 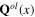 around the background characterized by the functions
around the background characterized by the functions 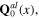
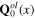 and considered as the physical vacuum of the system
and considered as the physical vacuum of the system

It can be shown that in terms of 
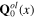 and
and 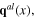
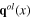 the action functional (57) has expression
the action functional (57) has expression
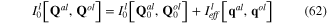
where ![$I_{eff}^{l}[{{{\bf q}}^{al}},{{{\bf q}}^{ol}}]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn100.gif) is the effective action functional of the fluctuation longitudinal phonon fields
is the effective action functional of the fluctuation longitudinal phonon fields  and
and  It has following quadratic from
It has following quadratic from
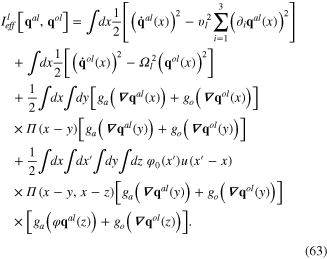
Since the fluctuation of longitudinal phonon fields generates the quasiparticles participating in various dynamical processes, the fluctuating longitudinal phonon fields 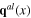 and
and 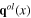 will be called dynamical longitudinal phonon fields.
will be called dynamical longitudinal phonon fields.
In order to exhibit the property of these fields to be longitudinal let us use following modified Fourier expansion
so that
In terms of the modified Fourier transforms  the action functional (63) becomes
the action functional (63) becomes
where  and
and  are the Fourier transforms of functions
are the Fourier transforms of functions  and
and 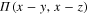 :
:

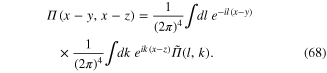
For evidently demonstrating main features of the total action functional (66) let us consider the case of the homogeneous electron gas with a constant electron density n(x) = n0 = const. It can be shown that in this case
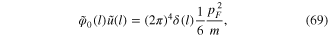
where pF is the electron momentum at the Fermi level, and formula (66) of the total action functional becomes
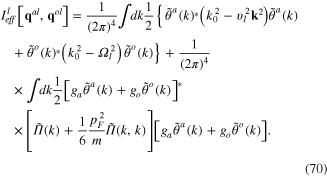
Thus the total action functional of longitudinal phonon fields in the harmonic approximation consists of two parts
where
can be considered as the action functional of a system of two scalar fields  and
and  describing longitudinal acoustic and optic phonons, whose Fourier transforms are the functions
describing longitudinal acoustic and optic phonons, whose Fourier transforms are the functions 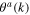 and
and 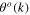 in formula (70),
in formula (70),

and
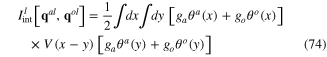
with
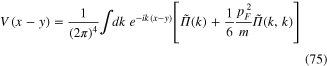
is the interacting functional describing the elastic scattering of phonons in the effective potential field V(x − y) as well as the mixing between longitudinal acoustic and optic phonons. Note that the effective potential V(x − y) is both non-local and non-instantaneous.
Since plasmons are generated by the fluctuation ζ(x) of the collective oscillation field φ(x) around its static background φ0(x), in order to study the plasmon–phonon interaction first we derive the expression of the action functional ![$I_{\operatorname{int}}^{fl}[\zeta ;{{{\bf Q}}^{a\mu }},{{{\bf Q}}^{o\mu }}]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn114.gif) of the interaction between the fluctuation field and phonon fields. We have
of the interaction between the fluctuation field and phonon fields. We have
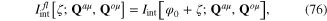
where ![${{I}_{\operatorname{int}}}[\varphi ;{{{\bf Q}}^{a\mu }},{{{\bf Q}}^{o\mu }}]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn115.gif) is determined by formulae (50) and (51). Because the terms containing transverse phonon fields are very small, we discard them and retain only the terms containing longitudinal fields. According to formula (61) each of them consists of two parts: the background longitudinal field
is determined by formulae (50) and (51). Because the terms containing transverse phonon fields are very small, we discard them and retain only the terms containing longitudinal fields. According to formula (61) each of them consists of two parts: the background longitudinal field 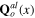 or
or 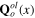 and the dynamical longitudinal phonon field
and the dynamical longitudinal phonon field 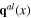 or
or  Consider again the case of homogeneous electron gas. Then in the harmonic approximation with respect to both types of fields (fluctuation field and phonon fields) the action functional can be represented in the general form as follows:
Consider again the case of homogeneous electron gas. Then in the harmonic approximation with respect to both types of fields (fluctuation field and phonon fields) the action functional can be represented in the general form as follows:
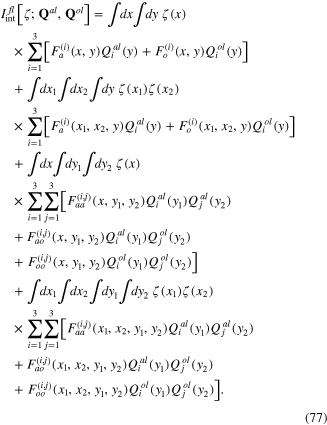
The Fourier transform  of the fluctuation field
of the fluctuation field 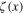 is expressed in terms of the Fourier transform
is expressed in terms of the Fourier transform 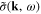 of the fluctuation field
of the fluctuation field  according to formula (48), i.e.
according to formula (48), i.e.
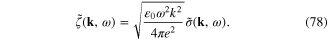
Therefore between  and
and  there exists following linear functional relation
there exists following linear functional relation
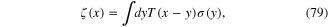
where
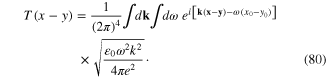
Similarly, according to formula (64), between the dynamical longitudinal phonon fields 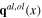 and the scalar fields
and the scalar fields  there exists following linear functional relation
there exists following linear functional relation
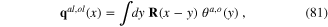
where
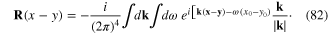
It is straightforward to derive the expression of the action functional of the interaction of plasmon with longitudinal phonons from formulae (61), (77), (79) and (81).
5. Quantum fields of interacting plasmon–photon–phonon system
On the basis of the results obtained in preceding sections we consider now the whole system of interacting plasmon, photon and phonons. The total action functional of this system has the expression (37). The collective oscillation scalar filed φ(x) is split into two parts: the static background field φ0(x) and the fluctuation field ζ(x). Each longitudinal phonon field 
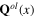 is also split into two parts: the static background field
is also split into two parts: the static background field 
 and the dynamical longitudinal phonon fields
and the dynamical longitudinal phonon fields 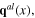
 while the transverse phonon fields
while the transverse phonon fields 
 themselves are the dynamical ones without the background fields:
themselves are the dynamical ones without the background fields:  and
and 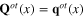 .
.
Plasmon is the quantum of a Hermitian scalar field σ(x) called plasmon field. The longitudinal phonons can be considered as the spinless quasiparticles. The scalar fields 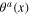 and
and 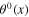 having these spinless quasiparticles as their quanta are called effective longitudinal phonon fields. In order to shorten lengthy formulae, they are introduced and used instead of the original longitudinal vector fields
having these spinless quasiparticles as their quanta are called effective longitudinal phonon fields. In order to shorten lengthy formulae, they are introduced and used instead of the original longitudinal vector fields 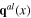 and
and 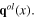 Meanwhile the transverse acoustic and optic phonon are the quanta of the original transverse vector fields
Meanwhile the transverse acoustic and optic phonon are the quanta of the original transverse vector fields 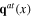 and
and 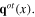 Above-mentioned quantized fields have following expansions in terms of the destruction and creation operators of the corresponding quasiparticles:
Above-mentioned quantized fields have following expansions in terms of the destruction and creation operators of the corresponding quasiparticles:
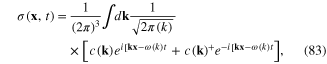
where c(k) and c(k)+ are the destruction and creation operators of the plasmon with momentum k, and ω(k) is its energy,
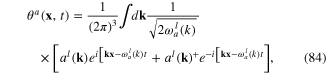
and
where al(k) or bl(k) and al(k)+ or bl(k)+ are the destruction and creation operators, respectively, of the longitudinal acoustic or optic phonon with momentum k and energy  or
or  ,
,

and
where  or
or  and
and  or
or 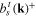 are the destruction and creation operators, respectively, of the transverse acoustic or optic phonon with momentum k, energy
are the destruction and creation operators, respectively, of the transverse acoustic or optic phonon with momentum k, energy 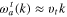 or
or 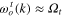 and polarization vector
ξ
(s)(k), s being the index indicating the polarization state of the transverse phonons with momentum k
and polarization vector
ξ
(s)(k), s being the index indicating the polarization state of the transverse phonons with momentum k
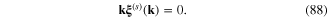
The total action functional of the system of interacting plasmon, photon and phonons has the expression of the form
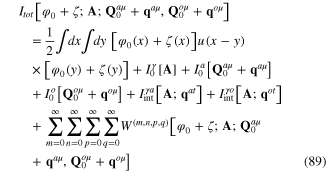
with  After the quantization procedure the fluctuation field ζ(x), the fluctuating longitudinal phonon fields
After the quantization procedure the fluctuation field ζ(x), the fluctuating longitudinal phonon fields 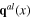 and
and 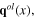 the transverse phonon fields
the transverse phonon fields 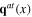 and
and  become the field operators, while the background fields φ0(x),
become the field operators, while the background fields φ0(x),  and
and 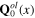 remain to be classical fields. Quantum fluctuation field is expressed in terms of the plasmon quantum field σ(x) through the linear functional relation (79), longitudinal phonon fields are expressed in terms of the longitudinal phonon effective scalar fields
remain to be classical fields. Quantum fluctuation field is expressed in terms of the plasmon quantum field σ(x) through the linear functional relation (79), longitudinal phonon fields are expressed in terms of the longitudinal phonon effective scalar fields 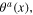
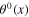 by means of the linear functional relation (81). The quantum of σ(x) is plasmon, the quanta of
by means of the linear functional relation (81). The quantum of σ(x) is plasmon, the quanta of  are longitudinal phonons, and the quanta of
are longitudinal phonons, and the quanta of  are transverse phonons. Thus in the whole system of interacting plasmon, photon and phonons there are three types of dynamical fields:
are transverse phonons. Thus in the whole system of interacting plasmon, photon and phonons there are three types of dynamical fields:
- (1)Fluctuation field ζ(x),
- (2)Transverse electromagnetic field A(x),
- (3)Longitudinal as well as transverse acoustic and optic phonon fields

 and
and 
 .
.
The total action functional of the whole system can be represented in the form

where the first term in rhs of equation (90) is the action function of free fields and second term is the interaction action functional. Action functional of free fields is the sum of action functional of all six free dynamical fields
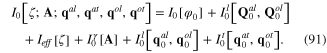
All six terms in rhs of equation (91) were given in preceding sections. The expression of interaction action functional has the general form
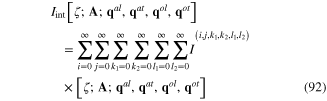
The term ![${{I}^{(i,j,{{k}_{1}},{{k}_{2}},{{l}_{1}},{{l}_{2}})}}[\zeta ;{\bf A};{{{\bf q}}^{al}},{{{\bf q}}^{at}},{{{\bf q}}^{ol}},{{{\bf q}}^{ot}}]$](https://content.cld.iop.org/journals/2043-6262/6/3/035003/revision1/ansn511832ieqn167.gif) is a homogeneous functional polynome of ith, jth, k1-th, k2-th, l1-th and l2-th orders with respect to the functional variables ζ(x), A(x), qal(x), qat(x), qol(x) and qot(x), respectively.
is a homogeneous functional polynome of ith, jth, k1-th, k2-th, l1-th and l2-th orders with respect to the functional variables ζ(x), A(x), qal(x), qat(x), qol(x) and qot(x), respectively.
According to formulae (79) and (81), the fluctuation field ζ(x) is a linear functional of plasmon field σ(x), and longitudinal phonon fields  are the linear functional of two effective scalar phonons as two spinless quasiparticles. Substituting rhs of formulae (79) and (81) into the expression (92), we obtain the interaction action functional in the form of a functional of the scalar fields σ(x),
are the linear functional of two effective scalar phonons as two spinless quasiparticles. Substituting rhs of formulae (79) and (81) into the expression (92), we obtain the interaction action functional in the form of a functional of the scalar fields σ(x), 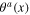 and
and  of plasmon and longitudinal phonons, and transverse vector fields
of plasmon and longitudinal phonons, and transverse vector fields  and
and  of transverse phonons.
of transverse phonons.
In the diagrammatic representation of the finally derived expression of the interaction action functional, each term is represented by a corresponding vertex with definite external lines. The number of external lines of each type indicate the number of corresponding particles or quasiparticles participating in the represented interaction fact.
6. Conclusion and discussions
In the present work, by means of the powerful functional integral technique, the quantum fields of the interacting system of plasmons, photons and phonons in electron gas of solids were constructed. The starting assumptions are the fundamental principles of electrodynamics and quantum theory of many-body systems. The general form of the formula of total action functional was established. The whole system is described by a set of six fields: the scalar plasmon field σ(x), transverse electromagnetic field A(x), the effective scalar fields  and
and 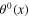 of longitudinal phonons as spinless quasiparticles, the transverse phonon vector fields
of longitudinal phonons as spinless quasiparticles, the transverse phonon vector fields 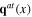 and
and 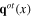 ,
,
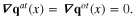
The total interaction action functional of the whole system is a series in which each term represents a definite interaction fact.
The derived interaction action functional has following particular feature: all terms in its expression represent the non-local and non-instantaneous interaction between the involved quantum fields. The Lagrangian and Hamiltonian similar to those in traditional quantum field theory do not exist. Although each term in the expression of the interaction action functional is the matrix element of a physical process in the first order approximation, the matrix elements of physical processes in higher order approximations cannot be calculated by means of the traditional perturbation theory. Therefore it is necessary to elaborate the new method for calculating the matrix elements of physical processes in higher orders from the formula of total action functional derived in the present work. Thus a lot of theoretical works should be performed in order to fulfill the construction of a complete quantum theory of physical phenomena and processes with the participation of plasmon.
Acknowledgement
The authors would like to express their sincere gratitude to Vietnam Academy of Science and Technology for the support.