Abstract
Transferring a quantum state from one location to another without physically sending the state itself through open space is a special global task that can only be carried out thanks to the laws of nature, namely the principles of quantum mechanics. In this work, we devise protocols for two senders to jointly prepare the most general two-qubit state for a receiver under the supervision of a controller by using three different types of quantum channels, all of which are non-maximally entangled. First, we propose the schemes to produce the quantum channels concerned, and then we present the concrete steps required to execute the protocols, highlighting the issue of why shared non-maximal entanglement is intentionally used instead of maximal entanglement.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
One of the most specific and also most important concepts in quantum information sciences is quantum entanglement [1] which Schrödinger singled out many decades ago as 'the characteristic trait of quantum mechanics'. It lies at the heart of quantum mechanics and is now viewed as a useful resource for quantum information processing and quantum computing. With its help, a number of classically impossible tasks can be done quantumly (i.e. in a way based on the postulates of quantum mechanics), such as unconditionally secure cryptography [2], superdense coding [3], quantum secret sharing [4], quantum dialogue [5] and so on. Most notably, in 1993 Bennett et al proposed for the first time a highly intriguing quantum protocol called teleportation [6] which allows one to securely and faithfully transfer an unknown single-qubit state from a sender to a distant receiver, without direct physical transportation of the state itself across space, by employing an Einstein–Podolsky–Rosen (EPR) pair [7] as the shared quantum channel. Soon after this, related works appeared widely and achieved great advancements in both theoretical [8] and experimental [9] aspects. As extensions of the teleportation scheme, two recognized versions are the remote state preparation (RSP) scheme [10], in which the sender knows the full identity of the to-be-prepared state, and the joint remote state preparation (JRSP) scheme [11], in which there is more than one sender and each sender is allowed to know only partial information of the state to be prepared, thus ensuring the secrecy of the target state since neither sender is able to learn the state identity. In addition, a set of controllable schemes such as controlled teleportation [12], controlled RSP [13] and controlled JRSP [14] have also been introduced to enhance the security. The essence of a controlled protocol is that a given task cannot be perfectly completed without permission of the controller, although they are not required to know the details of the state of concern. All of them can be performed with unit success probability and unit fidelity when maximal entanglement is used as the shared quantum channel along with the so-called feed-forward measurement strategy. If the quantum channel is non-maximally entangled, the fidelity may remain at one, but the success probability is often less than one [15]. Nevertheless, in certain circumstances non-maximal entanglement turns out to be necessary and, surprisingly, sometimes less entanglement proves to be more useful (see [16] and the references therein). As demonstrated in reference [17–19], using particular non-maximally entangled states can still provide both unit success probability and unit fidelity for controlled teleportation and controlled RSP. Such perfect features have also been achieved recently for controlled JRSP of an arbitrary single-qubit state [20]. Developing this idea, in this work we use three different types of non-maximally entangled states as the shared quantum channels for controlled JRSP of an arbitrary two-qubit state. The first, most trivial, quantum channel is two four-qubit non-maximally entangled states as considered in reference [20]. The second type of non-local resource comprises one Greenberger–Horne–Zeilinger (GHZ) state [21] and one four-qubit non-maximally entangled state. The last quantum channel type is a single seven-qubit non-maximally entangled state. We shall describe in detail how to produce the above-mentioned quantum channels and how to employ them to perform our task. Furthermore, we shall also consider a case when the controller is disabled by some objective reasons and analyze the dependence of the averaged fidelity on the parameters of the quantum channels concerned, indicating flexibility of the protocols.
This paper is structured as follows. After the introduction, section 2 considers three different non-maximally entangled states as the working quantum channels shared among the authorized participants. The main content is presented in section 3 where perfect protocols for controlled JRSP of the most general two-qubit state are devised. Section 4 provides discussion on a possible unwanted situation that prevents the protocols from being perfect, but retains a priori intended demand. Finally, we summarize our work in section 5.
2. The working quantum channels
The task we are concerned with involves four parties: two senders (Alice and Bob), one receiver (Charlie) and one controller (David). All four authorized participants are arbitrarily far apart from each other. The two-qubit state which needs be prepared at the receiver's location has the most general form
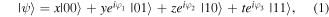
with real parameters x, y, z, t, 
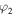 and
and  satisfying the normalization condition x2 + y2 + z2 + t2 = 1 and
satisfying the normalization condition x2 + y2 + z2 + t2 = 1 and  denotes a product state of two qubits, one of which is in the state
denotes a product state of two qubits, one of which is in the state  and the other in
and the other in 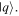 To keep the state
To keep the state 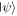 secret, neither sender is permitted to know the full set of x, y, z, t,
secret, neither sender is permitted to know the full set of x, y, z, t, 
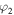 and
and 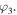 Instead, Alice knows only x, y, z and t, while Bob only
Instead, Alice knows only x, y, z and t, while Bob only 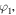
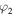 and
and 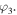 Moreover, the four parties are allowed to carry out only local actions (unitary operations and/or measurements) combined with reliable classical communication. They, therefore, should safely share some entangled quantum channel beforehand. The quantum channels we have chosen to fulfill our task in this work are three new non-maximally entangled states, labeled
Moreover, the four parties are allowed to carry out only local actions (unitary operations and/or measurements) combined with reliable classical communication. They, therefore, should safely share some entangled quantum channel beforehand. The quantum channels we have chosen to fulfill our task in this work are three new non-maximally entangled states, labeled 
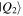 and
and  which have the following forms:
which have the following forms:

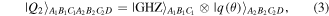
with
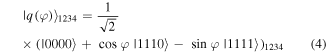
and
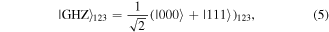
while
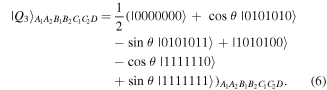
In the above quantum channels Alice holds two qubits A1, A2, Bob two qubits B1, B2, and Charlie two qubits C1, C2, while David holds two qubits D1, D2 in the case of  but just one qubit D in the cases of
but just one qubit D in the cases of 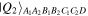 or
or  As is clear from equations (2), (3) and (6), the quantum channel states are characterized by the angles
As is clear from equations (2), (3) and (6), the quantum channel states are characterized by the angles 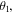
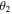 or
or 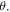 The entanglement between the senders and the receiver is always present independent of
The entanglement between the senders and the receiver is always present independent of 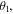
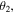
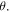 However, the entanglement between the controller and the others is sensitive to
However, the entanglement between the controller and the others is sensitive to 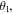
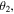
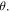 For the values of those angles for which the sine is equal to 0 the qubit(s) of David is (are) totally disentangled from the other ones, thus annulling his role as a 'quantum' controller. On the other hand, for other values of the angles, the states (2), (3) and (6) possess some degree of entanglement between David and the remaining group of participants, justifying him as a 'quantum' controller. In particular, for the values of the angles for which the sine is equal to ±1, the degree of that entanglement is maximal. Here, the relevant values of
For the values of those angles for which the sine is equal to 0 the qubit(s) of David is (are) totally disentangled from the other ones, thus annulling his role as a 'quantum' controller. On the other hand, for other values of the angles, the states (2), (3) and (6) possess some degree of entanglement between David and the remaining group of participants, justifying him as a 'quantum' controller. In particular, for the values of the angles for which the sine is equal to ±1, the degree of that entanglement is maximal. Here, the relevant values of 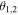 and
and 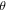 are such that the sine is different from 0 and ±1. Of importance is the fact that the values of
are such that the sine is different from 0 and ±1. Of importance is the fact that the values of 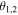 or
or 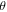 are consciously assigned only to the controller David. This obviously enhances the security level because even if the qubits of David and Charlie are unexpectedly captured by Eve, a malicious enemy, the identity of the target state (1) remains undiscovered by Eve as she has no idea about the angles and hence is unable to decide the correct recovery actions (see later). Production of the state
are consciously assigned only to the controller David. This obviously enhances the security level because even if the qubits of David and Charlie are unexpectedly captured by Eve, a malicious enemy, the identity of the target state (1) remains undiscovered by Eve as she has no idea about the angles and hence is unable to decide the correct recovery actions (see later). Production of the state 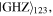 equation (5), had long been well-known [21] and that of the state
equation (5), had long been well-known [21] and that of the state 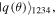 equation (4), was devised in reference [20]. So the states
equation (4), was devised in reference [20]. So the states 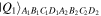 and
and 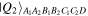 in equations (2) and (3) are readily producible. As for the state
in equations (2) and (3) are readily producible. As for the state 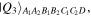 equation (6), we propose to produce it using a quantum circuit shown in figure 1 by means of single-qubit Hadamard gates:
equation (6), we propose to produce it using a quantum circuit shown in figure 1 by means of single-qubit Hadamard gates:
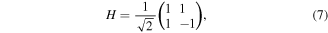
single-qubit rotations:

both of which are written in the qubit's computational basis 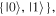 and two-qubit controlled-NOT gates:
and two-qubit controlled-NOT gates:
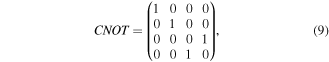
which is written in the qubits' computational basis 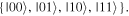 We are now in the position to employ the above-listed quantum channels for our purpose.
We are now in the position to employ the above-listed quantum channels for our purpose.
Figure 1. Quantum circuit for producing the seven-qubit non-maximally entangled state in equation (6). The circuit is read from left to right and each single line denotes a qubit.
Download figure:
Standard image High-resolution image3. The controlled JRSP protocols
In order to obtain unit success probability, our schemes, which we shall describe in detail in this section using each of the three above-mentioned quantum channels, are performed by four sequential steps as follows.
In the first step, Alice applies to her two qubits A1 and A2 a unitary operator U, which for the quantum channel states (2) and (3) is defined by

while for the quantum channel state (6) it reads

both are written in the computational basis of two qubits A1 and A2: 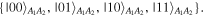 Then, she measures them in that basis to find a state
Then, she measures them in that basis to find a state 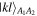 with
with 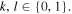 After measuring, she publicly announces the obtained outcomes kl.
After measuring, she publicly announces the obtained outcomes kl.
The second step is tricky in the sense that the feed-forward measurement strategy will be exploited. Concretely, in this step Bob's correct action depends essentially on Alice's measurement outcomes kl. Namely, if kl = 00, he needs to apply to his qubits 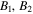 the following unitary operator:
the following unitary operator:
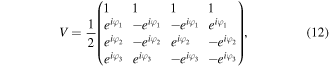
which is written in the computational basis 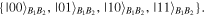 However, the correct unitary operator should be
However, the correct unitary operator should be
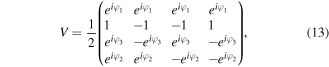
if kl = 01,
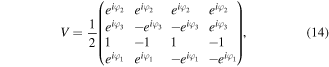
if kl = 01 and
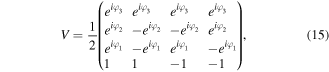
if kl = 11. Afterwards, Bob measures his qubits in their computational basis to find a state 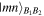 with
with  The obtained outcomes mn will also be publicly announced after the measurement.
The obtained outcomes mn will also be publicly announced after the measurement.
The third step will be done by David which is subject to the quantum channel used. For the quantum channel (2) David first applies 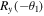 to qubit D1 and
to qubit D1 and 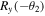 to qubit D2 (that is, he rotates qubit D1 by an angle
to qubit D2 (that is, he rotates qubit D1 by an angle 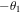 and qubit D2 by an angle
and qubit D2 by an angle 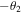 around the y-axis), then measures those qubits in their computational basis
around the y-axis), then measures those qubits in their computational basis 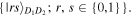 Yet, in the case of using the states (3) or (6) as quantum channels, David just rotates qubit D by an angle
Yet, in the case of using the states (3) or (6) as quantum channels, David just rotates qubit D by an angle 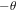 around the y-axis followed by measurement of it in the computational basis
around the y-axis followed by measurement of it in the computational basis 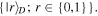 It is worth noting that only David can do the aforementioned rotation(s) because, as devised, nobody else except him knows the exact values of the rotation angle(s). This is the figure of merit to be highlighted regarding the use of non-maximally entangled states (2), (3) or (6), which yield a security level higher than that of using maximally entangled quantum channels. Of course, as a rule, after finishing the measurement David is required to inform Charlie of his outcomes rs or r (or simply make them public through a classical communication channel), depending on which quantum channel was actually in use.
It is worth noting that only David can do the aforementioned rotation(s) because, as devised, nobody else except him knows the exact values of the rotation angle(s). This is the figure of merit to be highlighted regarding the use of non-maximally entangled states (2), (3) or (6), which yield a security level higher than that of using maximally entangled quantum channels. Of course, as a rule, after finishing the measurement David is required to inform Charlie of his outcomes rs or r (or simply make them public through a classical communication channel), depending on which quantum channel was actually in use.
Finally, in the fourth step, after collecting the outcomes of all the necessary measurements from Alice, Bob and David, Charlie is able to transform the state of her qubits to the target one by applying the recovery operators R1 and R2 to the qubits C1 and C2, respectively. The correct recovery operators differ depending on the quantum channels used. For our protocols we have been able to work out explicit and compact formulae for the recovery operations. Precisely, if the quantum channel is via the state (2), then
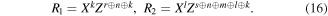
However, if it is the state (3), then
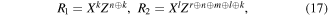
and otherwise (i.e. the state (6) serves as the quantum channel)
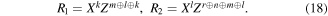
In the above recovery operators ⨁ stands for addition mod 2, while
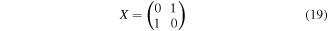
and

are the well-known Pauli bit-flip and phase-flip operators. The fidelity is clearly one. The total success probability is also one because Charlie is able to obtain the desired state for any possible set of the measurement outcomes via whatever quantum channel. Our protocols are therefore perfect despite using non-maximally entangled states as the working quantum channel. The steps for implementing our controlled JRSP protocols are schematically sketched in figure 2 when the state (2) is used and in figure 3 when the state (3) or the state (6) serves as the shared quantum channel.
Although anyone can obtain the broadcasted measurement outcomes, not everyone can benefit from the classical information, thus guaranteeing the security of our protocols.
Figure 2. Scheme for the controlled joint remote preparation of a general two-qubit state by using the quantum channel in equation (2). Each single line denotes a qubit, while a double line denotes the publicly broadcasted classical communication which costs two bits.
Download figure:
Standard image High-resolution imageFigure 3. Scheme for the controlled joint remote preparation of a general two-qubit state by using the quantum channel in equations (3) or (6). Each single line denotes a qubit, while a double line denotes the publicly broadcasted classical communication which costs two bits.
Download figure:
Standard image High-resolution image4. Discussion
As presented above, our controlled JRSP protocols are perfect (with unit fidelity, unit success probability and absolute security). Nevertheless, there are many situations that prevent the protocols from obtaining perfection. In this section we shall address a situation that might occur in practice. Suppose that David's qubits D1, D2 (or D) are, for some reason, lost or captured by an unauthorized party during the entanglement distribution process and the authorized parties are aware of this accident. In this case one may ask: 'how close to the target state could the state at Charlie's location be?' Let us analyze this. The above-mentioned accident can be treated as the removal of the controller's participation. Mathematically, this is tantamount to tracing out over the controller's qubits. As a consequence, what will be at hand to Charlie is a mixed state specified by a reduced density matrix 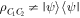 which Charlie would obtain via the steps described in the previous section, but without David's participation (i.e. the third step is skipped). The fidelity f of the state at hand to Charlie's as compared to the target state
which Charlie would obtain via the steps described in the previous section, but without David's participation (i.e. the third step is skipped). The fidelity f of the state at hand to Charlie's as compared to the target state 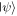 in equation (1) is given by
in equation (1) is given by
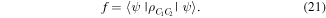
Our calculations yield
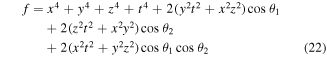
when using the quantum channel (2) and
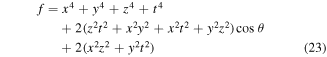
when the quantum channel (3) or (6) is used. From equations (22) and (23) we see that the fidelities depend not only on the quantum channel, but also on the state to be prepared. Of interest then is the averaged fidelity  (i.e. the fidelity which is averaged over all the possible input states). To obtain an explicit analytical expression, we set
(i.e. the fidelity which is averaged over all the possible input states). To obtain an explicit analytical expression, we set 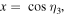
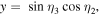
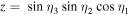 and
and 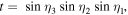 with new angles
with new angles 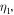
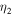 and
and 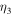 . The averaged fidelity can then be calculated using the following formula [22]:
. The averaged fidelity can then be calculated using the following formula [22]:
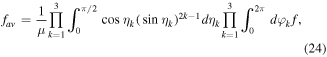
where ![${\eta }_{k}\in [0,\pi /2],{\varphi }_{k}\in [\mathrm{0,\; 2}\pi ),k=\{\mathrm{1,\; 2,\; 3}\}$](https://content.cld.iop.org/journals/2043-6262/7/2/025007/revision1/ansnaa1dabieqn64.gif) and
and 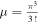 is the total volume of the manifold of pure states [22]. Substituting f from equations (22) or (23) into equation (24) and carrying out the integrations we obtain
is the total volume of the manifold of pure states [22]. Substituting f from equations (22) or (23) into equation (24) and carrying out the integrations we obtain
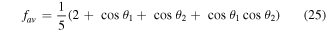
for the quantum channel (2) and
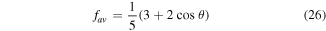
for the quantum channel (3) or (6). The expressions (25) and (26) imply that the closeness between 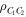 and
and 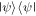 can be tailored by the angles θ or
can be tailored by the angles θ or 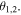 The dependence of
The dependence of 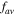 on
on  and θ are displayed in figures 4 and 5, respectively. At that point we notice that the best value of the fidelity that can be obtained only by classical means is equal to
and θ are displayed in figures 4 and 5, respectively. At that point we notice that the best value of the fidelity that can be obtained only by classical means is equal to  [23]. Now, as in the visual from figures 4 and 5, there are domains of
[23]. Now, as in the visual from figures 4 and 5, there are domains of  or θ in which
or θ in which 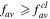 or
or  So, the values of
So, the values of 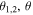 could be on-purpose chosen properly in order that, even if the qubits D1,2 or D are accidentally lost or captured by an unauthorized party, the fidelity
could be on-purpose chosen properly in order that, even if the qubits D1,2 or D are accidentally lost or captured by an unauthorized party, the fidelity 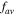 is greater than, equal to or smaller than
is greater than, equal to or smaller than 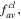 depending on a pre-established demand.
depending on a pre-established demand.
Figure 4. The dependence of the averaged fidelity fav, equation (25), on the angles θ1 and θ2. The plane at 2/5 represents the classical limit of the averaged fidelity.
Download figure:
Standard image High-resolution imageFigure 5. The dependence of the averaged fidelity fav, equation (26), on the angles θ. The horizontal line at 2/5 represents the classical limit of the averaged fidelity.
Download figure:
Standard image High-resolution imageReturning to our protocols we see that the classical communication cost needed to broadcast the measurement outcomes is 6 bits when using the quantum channel (2) and 5 bits when using the channel (3) or the channel (6). As for the quantum resource, the channel (2) requires 8 qubits, 2 Hadamard gates, 8 CNOTs and 4 rotations, the channel (3) requires 7 qubits, 2 Hadamard gates, 5 CNOTs and 2 rotations, while the channel (6) requires 7 qubits, 2 Hadamard gates, 7 CNOTs and 2 rotations. An overall assessment, especially taking into account the fact that the CNOT gate is much more expensive than the Hadamard gate and rotation, indicates that use of the quantum channel (3) proves to be cheaper than that of the other two.
5. Conclusion
To summarize, we have considered three distinct non-maximally entangled quantum channels, equations (2), (3) or (6), proposed their production schemes and devised protocols for two parties to jointly prepare the most general two-qubit state for a third party under 'quantum' control of a fourth party. This is a truly global quantum task because all the participants may be space-like. We have shown that these protocols in ideal conditions are perfect in the sense that both the fidelity and success probability are equal to one. The advantages of using non-maximally entangled quantum channels are an enhancement of security level and provide the flexibility of choosing the parameters of the quantum channels so that a pre-demanded averaged fidelity can be achieved even in case when the controller's qubits are lost en route. In this sense our protocols are flexible. Furthermore, we have also assessed the overall cost of each of the protocols and found that the quantum channel (3) is the most advantageous.
Acknowledgments
This work is supported by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under project No.103.01-2014.02.






